The Shape of Tensor
Tensors are the primary data structures used by neural networks. And they are rather fascinating as well. Machine learning and by extension deep learning is an interdisciplinary field. Its interesting to note how many different people from many different fields came to same concepts. Specific to this writing, the concept of tensors.
The concept of tensor is a mathematical generalization of more specific concepts, vectors and matrices in particular.
In neural networks transformations, input, output etc are performed via tensors.
To build a good enough concept let's start with a matrix of some simple concepts from computer science and mathematics.

The same can also be represented via following matrix
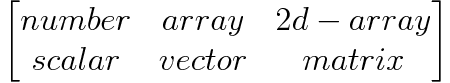
This pseudo-mathematical notation gives us a nice one-to-one relationship between concepts of number, array and 2d-array from computer science to the concepts of scalar, vector and matrix in mathematics.
Let's write examples of above 6 concepts to better understand them
number ---> 9
scalar ---> 9
array ---> [5, 8, 3]
vector ---> (5i, 8j, 3k)
or
5i + 8j + 3k
or simply
(5, 8, 3)
2d-array ---> [
[1, 2, 3]
[4, 5, 6]
[7, 8, 9]
]
matrix ---> |1, 2, 3|
|4, 5, 6|
|7, 8, 9|
The index notation
Upon closer inspection of the above examples it's apparent that to access any element in each representation, we need the same number of indices in the related concepts of computer science and mathematics.
For example, to access an element in an array we need following notation
my_array = [5, 8, 3]
my_array[2] ---> 8
Similarly to access a component of a mathematical vector we need one index, and, vice-versa for matrix and 2d-array. We have following underlying pattern:
| Indices Required | Computer Science | Mathematics |
|---|---|---|
| 0 | number | scalar |
| 1 | array | vector |
| 2 | 2d-array | matrix |
This gives us a working framework to make the generalization.
Meet the tensors
When we have more than two indices to refer to a specific element in a data structures (or mathematical, structure) we stop treating them with special names like scalars, vectors, matrices etc. Instead we address them with a more generalized language.
We call them Tensors.
This gives us following table
| Indices Required | Computer Science | Mathematics |
|---|---|---|
| 0 | number | scalar |
| 1 | array | vector |
| 2 | 2d-array | matrix |
| n | nd-array | tensor |
For all practical purposes in programming. It is good enough to remember that:
Tensors are multidimensional arrays.
Coming back to the part of generalization part. It's safe to draw following conclusions:
- scalar ---> 0 dimensional tensor ---> number
- vector ---> 1 dimensional tensor ---> simple array
- matrix ---> 2 dimensional tensor ---> 2d array
- nd array ---> n dimensional tensor ---> nd array
The dimension of a tensor a completely different entity from what we mean when we refer to the dimension of a vector in a vector space. The dimension of a tensor does not tell us how many components exist within the tensor.
If we have a three dimensional vector from three dimensional euclidean space, we have an ordered triple with three components.
A three dimensional tensor, however, can have many more than three components. Our two dimensional tensor 2d-array for example has nine components.
2d-array ---> [
[1, 2, 3]
[4, 5, 6]
[7, 8, 9]
]
Rank and Axes of Tensor
A tensor's rank is equal to the number of indices are needed to access to a specific element within the tensor.
In our example our 2d-array tensor is of rank two because we need to indices to access any element inside it.
elem = 2d-array[i][j]
Axis refers to a particular dimension of a tensor.
In case of a tensor of rank 2, it has 2 dimensions (also called 2 axis), hence a requirement of 2 indices (one for each axis or dimension) to access any element.
The length of each axis tells us how many indexes are available along each axis.
The Shape of Tensor
The shape of a tensor is determined by the length of each axis, so if we know the shape of a given tensor, then we know the length of each axis, and this tells us how many indexes are available along each axis.
The shape of a tensor gives us the length of each axis of the tensor.
Going back to our familiar 2d-array tensor
2d-array ---> [
[1, 2, 3]
[4, 5, 6]
[7, 8, 9]
]
We say that above tensor's shape is 3 x 3 which means that it has 2 axis (or dimensions) of length 3 each.
Tensor's shape is super important.
Higher rank tensors tend to become more and more abstract very quickly. In this case shape provides us some reference point to understand them.
Additionally tensors being the data structures of neural networks flow through various layers of the network. More than often they are required to be in a certain shape.
Reshaping the tensor
Reshaping is a simple yet very powerful concept. Simply put, reshaping refers to the process of changing the order of axis (dimensions) in the data structure. For example lets say we have a tensor of rank 2 as follows:
Shape 2 x 3
[
[4, 5, 6]
[7, 8, 9]
]
It can be reshaped to various shapes as follows:
Shape 6 x 1
[
[4],
[5],
[6],
[7],
[8],
[9],
]
Shape 3 x 2
[
[4, 7],
[5, 8],
[6, 9]
]
Shape 1 x 6
[
[4],[5],[6],[7],[8],[9],
]
Important point to note about reshaping operation is that it changes the shape, ie. it changes the ordering of individual elements inside a tensor, but is does not change the underlying elements themselves.
Above is a very crude but workable conceptual introduction to tensors.
It is by no means rigorous. However, it serves as good enough starting point while trying to work with Neural Networks from a "mathematically un-inclined programmer" perspective.
Rigorous mathematical treatment of this subject is of utmost importance if one wishes to do anything meaningful in the area of Deep Learning.
For a just enough introduction, this is a must read: Intruduction to Tensor Calculus, Kees Dullemond & Kasper Peeters.
I'll also highly recommend Tensor Calculus Made Simple, Taha Sochi
I enjoyed my time with the book. I hope you will too.